Sonne
Die Radiostrahlung der Sonne ist langwellige Fortsetzung ihrer thermischen Emission
im Optischen und Infrarot, die durch das warme und heiße Plasma erzeugt wird. Neben
einer zeitlich unveränderlichen 'ruhigen' Emission kommt es in Zeiten hoher Aktivität
auch zu einer kurz- oder längerfristig erhöhter Radioemission. Diese wird verursacht
durch Gebiete höherer Temperatur in den oberen Schichten sowie durch Wolken ausgestoßenen
Plasmas (CME 'Coronal Mass Ejections').
Die Schicht, die wir im sichtbaren Licht als Oberfläche bezeichnen könnten, ist die
Photosphäre, mit einer Temperatur von etwa 6000 K. Dies ist die tiefste Schicht, die
der direkten Beobachtung zugänglich ist, da hier wegen der mit der Tiefe ansteigenden
Dichte die Absorption des Sonnenplasmas ansteigt und damit tiefere Einblicke verhindert.
Die Temperatur nimmt mit der Höhe zunächst ab, bis etwa 4300 K, um dann in der
Chromosphäre wieder anzusteigen. Diese Schicht ist nur bei totalen Sonnenfinsternissen
in Emissionslinien zu beobachten. Oberhalb der Chromosphäre schließt sich die Ûbergangsschicht
('Transition Layer') an, in der die Temperatur von ca. 10000 K bis auf einige Hunderttausend K
ansteigt. Darüber liegt die Korona, mit sehr geringer Dichte und Temperaturen von
Millionen K, die sich bis einige Sonnenradien erstreckt.
Da das Absorptionvermögen des Sonnenplasmas zu längeren Wellenlängen hin zunimmt, kann man
im Radiobereich nicht mehr so tief in die Sonnenatmosphäre hineinschauen wie im sichtbaren
Licht. Somit kommt die Strahlung aus immer höheren Schichten, je tiefer die Frequenz ist.
Bei 10 GHz kann man bereits nur bis in die höhere Chromosphäre schauen, unterhalb von
1 GHz ist die Korona. In dieser Weise geben Radiobeobachtungen auf verschiedenen
Frequenzen Aufschluß über die Temperaturen in der verschiedenen Schichten. Die solaren
Radioflüsse werden täglich von einer weltweiten Kette von Radiosternwarten gemessen
und werden von NOAA
veröffentlicht. Im spektralen Verlauf des Radioflusses
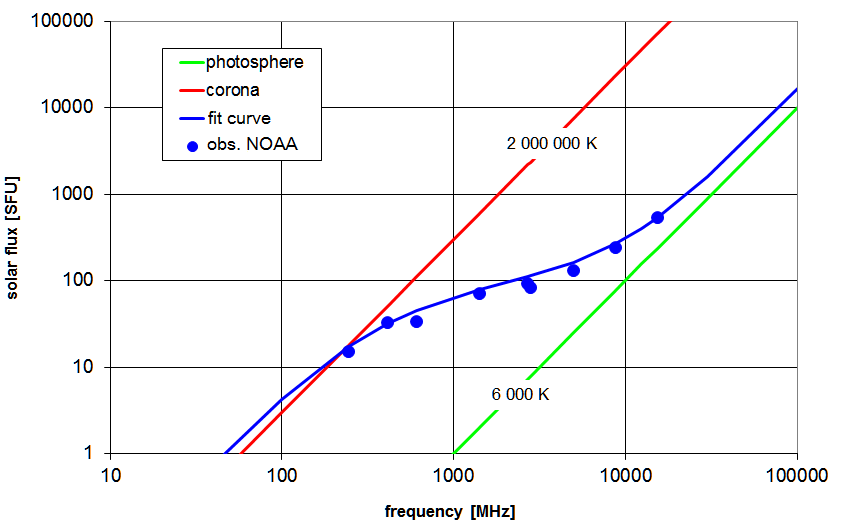
spiegelt sich die Temperaturschichtung in der Sonnenatmosphäre wieder:
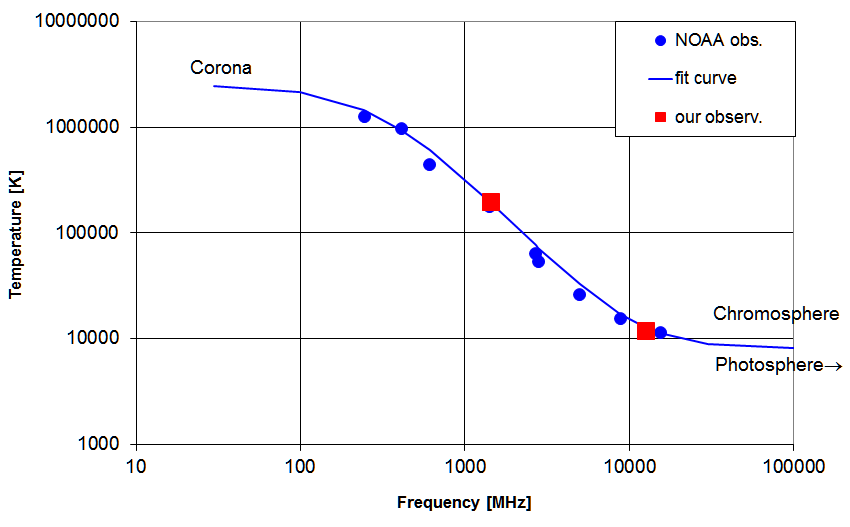
Bestimmung des Radioflusses der Sonne
Dazu sind vier Messungen erforderlich:
- direktes Signal: wenn die Antenne auf die Sonne gerichtet ist: p(Sonne)
- Himmelshintergrundes auf derselben Elevation: psky(ε)
- Flusskalibration: pcal
- Breite der Antennenkeule: HPBW
Alle Messungen kann man bequemerweise in einem Driftscan erhalten:
- Antenne wird auf die Position gerichtet, an der die Sonne in ca. 10 min sein wird
- die fortlaufende Registrierung hält den Anstieg des Signals fest, wenn die
Sonne in die Antennenkeule eintritt ...
- ... ein Maximum durchläuft (dies ergibt p(Sonne)) ...
- ... und wieder abnimmt.
- danach (oder am besten auch vorher) wird die Antenne auf eine Position gedreht,
die so weit von der Sonne entfernt ist, dass durch die Nebenkeulen keine
Sonneneinstrahlung erfolgt. Auf derselben Elevation ε wie der Sonne wird
der Hintergrund des 'leeren' Himmels gemessen: psky(ε)
- danach (oder am besten auch vorher) wird das Signal vom Fluskalibrator gemessen:
pcal
Dies kann so aussehen (auf 1.3 GHz). Die reichlich bemessenene Zeit vor und nach dem
Sonnendurchgang erlaubt es, die Nebenkeulen der Antenne zu erfassen.

Dieses Verfahren erfordert eine präzise Positionierung. Kann diese nicht erreicht werden,
wird man zunächst manuell nach dem maximalen Signal der Sonne suchen, um dann die Sonne bei
feststehender Antenne durch die Keule laufen zu lassen. Ein solch halber Driftscan erfüllt ebenso
seinen Zweck und erfordert weniger Zeit:
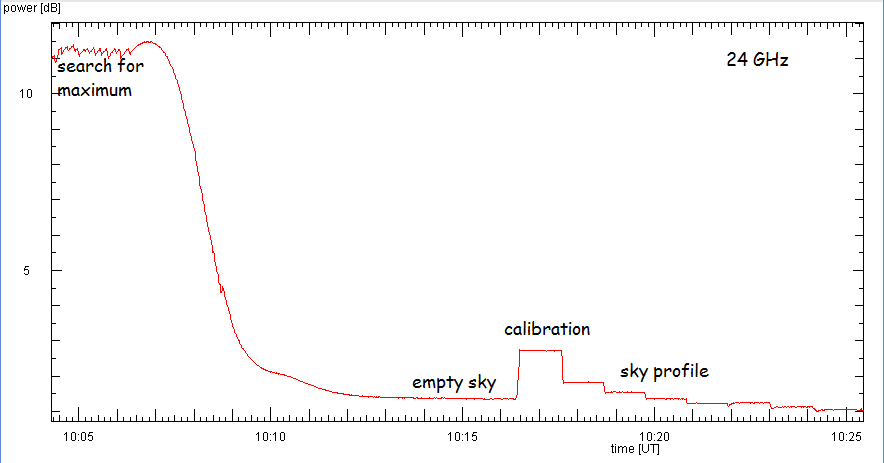
Auswertung
Hierbei geht man so vor: In den grundlegenden Beziehungen für das Sonnensignal (in linearer Leistung)
p(Sonne) = a (Tant(Sonne) + Tzenit/sinε + Tsys + TCMB)
und für den Himmelshintergrund
psky(ε) = a (Tzenit/sinε + Tsys + TCMB)
wird der unbekannte Skalierungsfaktor a durch die Flußkalibration ermittelt:
pcal = a (Tcal + Tsys)
- Verwendet man direkt den gemessenen Himmelshintergrund, so reicht die Kenntnis
der Systemtemperatur aus, um die Antennentemperatur der Sonne zu bestimmen:
Tant(Sonne) = (Tcal + Tsys)*(p(Sonne) - psky)/ pcal
- Sind aus einer ebenfalls durchgeführten Analyse des
Himmelshintergrundes die Systemtemperatur und Zenittemperatur bekannt - oder
können wegen der Stabilität des Systems als bekannt vorausgesetzt werden - kann man
auch diese Form verwenden:
Tant(Sonne) = (Tcal + Tsys)*p(Sonne)/pcal
- (Tzenit/sinε + Tsys + TCMB)
- Da z.B. auf 1 GHz die Zenittemperatur nur schwach wetterabhängig ist, kann man darüber hinaus
noch die Systemtemperatur bestimmen:
Tsys = (psky(ε) Tcal - pcal(Tzenit/sinε + TCMB)
/(pcal - psky(ε))
Radiofluss
Bei Kenntnis der effektiven Fläche Aeff der Antenne kann der solare
Radiofluss (in Jansky) berechnet werden:
FSonne = Aeff/2760 * Tant(Sonne)
Die erhaltene Antennentemperatur ist allerdings noch kein Maß für die physische Temperatur auf der Sonne, denn
sie hängt noch von den Eigenschaften der Antenne ab:
- ist die Sonnenscheibe mit ihrem Winkeldurchmesser von durchschnittlich D = 0.5º kleiner als die
Antennenkeule (d.h. HPBW) - bei den 1.3 GHz und 2.3 GHz Spiegeln - ist die wahre Temperatur auf der Sonnenoberfläche um den Füllfaktor
höher:
TSonne = 1.5393 * Tant(Sonne) * (HPBW/D)2
Der numerische Faktor ist eine Korrektur für die Form der Antennenkeule.
- Nur wenn die Sonne vollständig die Antennenkeule ausfüllt - bei den 10 GHz und 24 GHz Spiegeln -
sind Antennen- und wahre Temperatur
identisch:
TSonne = Tant(Sonne)
Half-Power Beam Width
Somit ist die Kenntnis der Breite der Antennenkeule notwendig. Da dies eine unveränderliche Eigenschaft
der Antenne ist, braucht sie nur einmal vermessen werden. Bei einem Driftscan fällt sie als Nebenprodukt
ab: die HPBW (Half-Power Beam Width) ist als die volle Breite auf dem Niveau in der halben Höhe des
Maximalwerts definiert. Da beim Driftscan die präzise Erdrotation zum Durchfahren der Keule in horizontaler
Richtung verwendet wird, misst man das Zeitintervall, in dem die Empfangsleistung = linear, und über dem
Hintergrund! - über dem halben Maximalwert liegt. Der in einer Stunde überstrichene Winkel beträgt
15º cos δSonne, wenn die Sonne bei der Deklination δSonne steht.
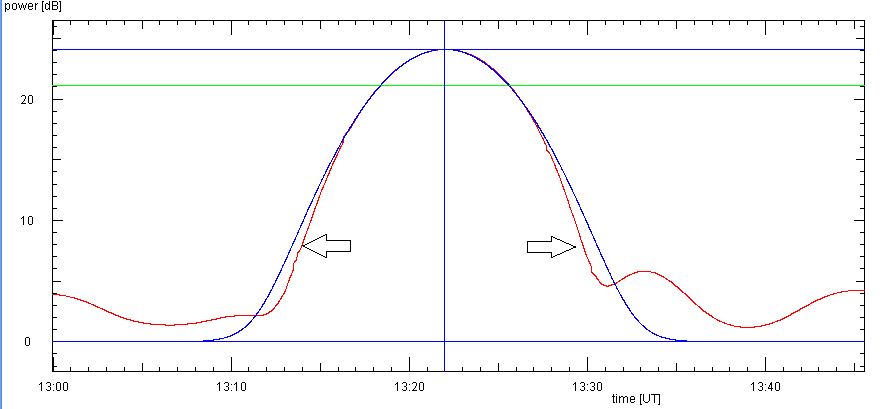
Eine weitere Möglichkeit besteht im Anpassen der Messkurve (rot) an ein Gauß-Profil (blau), wie unten
stehend gezeigt. Dabei läßt sich auch erkennen, wie gut die Antennenkeule einer Gaußfunktion nahekommt oder
von ihr abweicht. Die grüne Linie ist das Niveau der halben Maximalleistung, die schwarzen Pfeile deuten
an, bis wohin eine Registrierung der Hauptkeule reichen sollte.
Sonnenfinsternis 2015
|
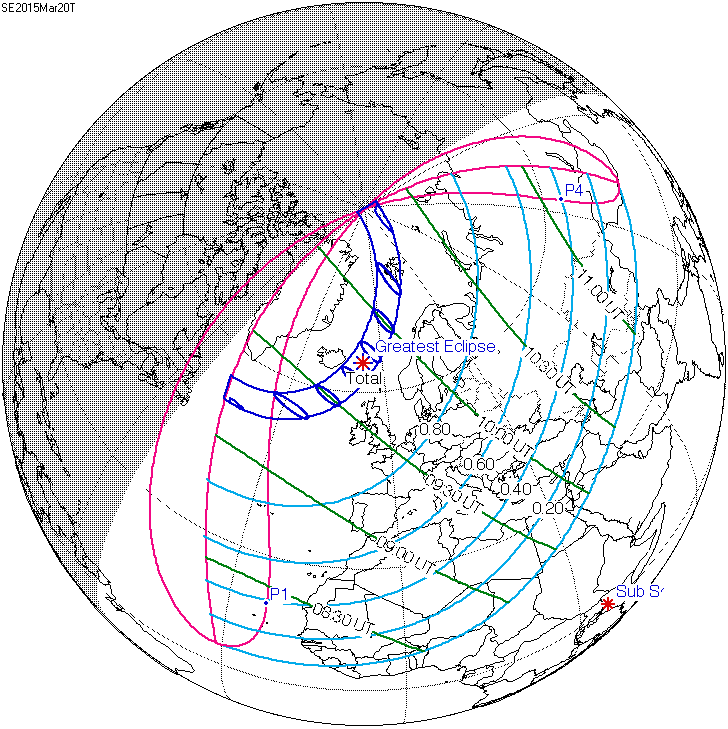
Die totale Sonnenfinsternis am 20. März 2015 hatte in Kiel um 09:46 UT die größte
Bedeckung von etwa 80 Prozent. Der erste Kontakt war um 08:38 und der letzte
um 10:56 UT ...
|

|
... aber der Hochnebel kam genau zur rechten Zeit, und so haben wir nichts gesehen.
Glücklicherweise konnte Hermann Fenger in unserer 'Zweigstelle' in Bielefeld durch
die Wolken ein Bild um 10:54 UT schießen. Brennweite 200 mm, Belichtungszeit 1/320 s
bei ISO 100 und Blende 7.
|

|
Aus den Wetterbildern von Meteosat im sichtbaren Licht
wurden Videofilme erstellt: Links ist die Erdscheibe während des gesamten Tages zu
sehen, rechts in Schwarzweiß wird gezeigt, wie der Halbschatten über Europa zieht.
Ein Klick auf das Bild startet den Film in einem Videobrowser.
Der Kernschatten ist zu klein, als dass er auf diesen Bildern zu erkennen ist. Der
Halbschatten ist dagegen mehrere tausend km groß.
Die Originalbilder haben eine Größe von 768 mal 576 Pixel. Die Aufzeichnung eines
Einzelbildes beträgt etwa 12 min, weil das Bild zeilenweise abgetastet wird.
Die Bilder, aufgenommen im zeitlichen Abstand 15 min, werden in Rönne in Videosequenzen
zusammengestellt.
|

|
|
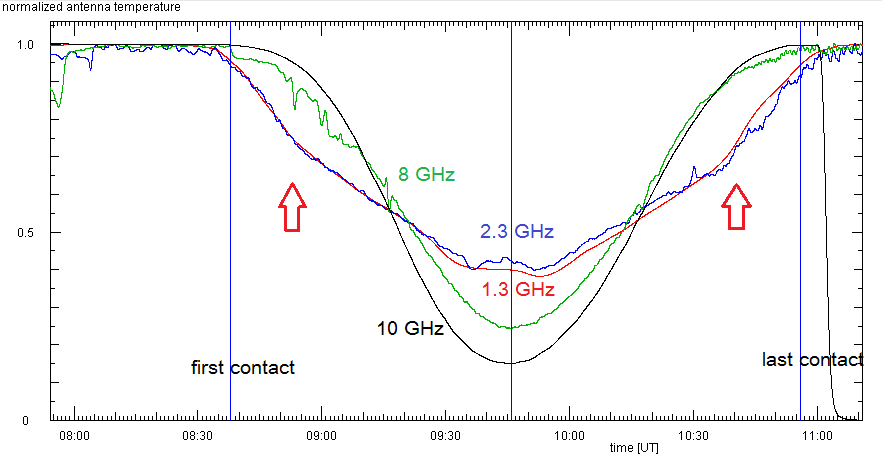
Bei DL0SHF haben wir die gesamte Finsternis auf 1.3, 2.3, 8.2, und 10 GHz beobachtet.
Das Diagramm zeigt den zeitlichen Verlauf der Antennentemperaturen, die auf den Wert
vor der Bedeckung normiert sind. Diese lineare Größe misst den Anteil des solaren
Radioflusses, der auf jeder Frequenz gemessen wurde. Man sieht:
- bei größter Bedeckung ist das Restsignal desto kleiner, je höher die Frequenz ist.
Bei höheren Frequenzen kommt die Radioemission aus den tieferen Schichten, nahe
der 'Oberfläche' der Sonne, der Photosphäre, aus der auch das sichtbare Licht
kommt. Auf tieferen Frequenzen entsteht die Radiostrahlung in der Korona, die
über der Photosphäre liegt.
- auf tiefen Frequenzen fällt das Signal eher ab als bei höheren, und auch vor dem
ersten Kontakt im sichtbaren Licht. Bei Frequenzen unterhalb etwa 3 GHz kommt die
Emission aus der Korona, die eine Region mit sehr heißem Gas ist und die sich
von oberhalb der Photosphäre bis in einige Sonnenradien Entfernung erstreckt.
Der Mond bedeckt diese außen liegende Schicht bevor er die Sonnenscheibe berührt.
- die Kurve bei 10 GHz ist 'V'-förmig, während sie bei 1.3 GHz mehr einem 'U' gleicht.
- auf 1.3 und 2.3 GHz hat die Kurve leichte Knicks (roter Pfeil deutet auf den Knick
nach der Finsternis) wo die Kurvensteigung sich etwas ändert ...
- ebenfalls auf 1.3 und 2.3 GHz gibt es zwei kleine Vertiefungen in der Nähe der maximalen
Bedeckung. Dass sie bei beiden Frequenzen gleichermassen auftauchen, zeigt dass sie
kein instrumenteller Defekt sind. Könnte dies durch eine Veränderung in der Erdatmosphäre
verursacht sein, wie dem Vorbeizug von Wolken?
|
|
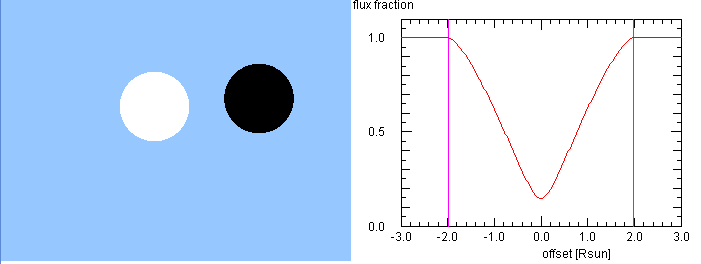
Hier sind die Erklärungen: im sichtbaren Licht und auch bei 10 GHz
ähnelt die Sonne einer Scheibe von fast gleichmäßiger Helligkeit. In der
nebenstehenden einfachen Modellierung der Finsternis bekommt man dann ein
'V'-förmigen zeitlichen Verlauf der gemessenen Helligkeit. Dazu wurde der Abstand
der Zentren von Mond und Sonne gewählt, dass sich eine größte Bedeckung von 80 Prozent
ergibt. Die Helligkeit fällt natürlich genau im Zeitpunkt des ersten Kontakts ab!
|
Zur interaktiven Simulation RadioEclipse
|
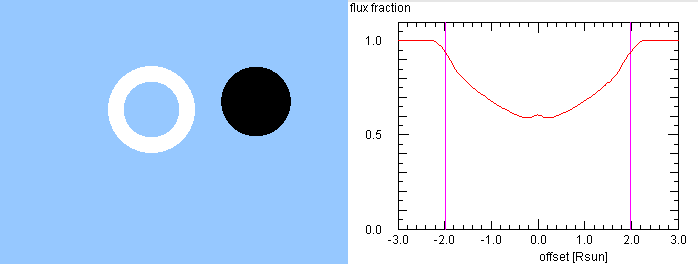
Auf 1.3 and 2.3 GHz entstammt die Radioemission der Korona, die oberhalb
der Photosphäre liegt. Wenn wir diese durch einen hellen Ring modellieren, dessen
Innenradius 0.8 und Außenradius 1.25 Radien der optischen Sonnenscheibe betragen,
erhalten wir:
- die Kurve hat 'U'-Form
- der Abfall des Signals beginnt noch vor dem ersten Kontakt, der durch den senkrechten
violetten Strich markiert ist
- Bei Abständen (offsets) von -1.5 und 1.5 Radien der Sonnescheibe ändert sich
die Steigung der Kurve etwas, aber deutlich. Dies entsteht durch die Bedeckung
des Rings durch den Mond, der etwas kleiner als die Außenrand des Rings ist.
- bei größter Bedeckung gibt es ein kleines Maximum im Signal. Dies entsteht, da
der Mond auch bei diesem Zeitpunkt nur die inneren Teile des Rings bedecken
kann, und somit tragen alle Teile des nunmehr vollständig freien Außenrandes
zum Signal bei
- vor und nach diesem Maximum gibt es zwei kleine Einbuchtungen, so wie sie
auf 1.3 und 2.3 GHz beobachtet werden. Daher sind diese Dellen nicht etwa
vorbeiziehenden Wolken der Erde, sondern die Folge der Bedeckung der ringförmigen
Emission der Korona durch die Mondscheibe. Sie sind die Folge der Bedeckung
einer Aufhellung der Korona auf ihrer Ostseite.
|
mehr Details im: Report on Observations, Data Reduction, and first Interpretation
und hier: Report on Modeling of the Observations
|
|
|
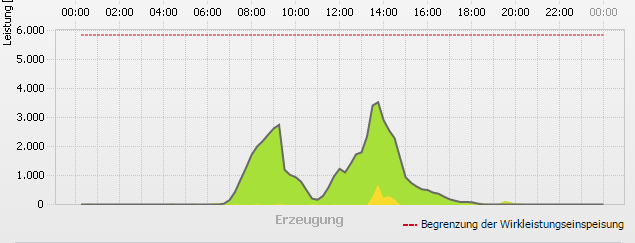
Trotz des grauen Himmels über Schleswig-Holstein gibt die Aufzeichnung der Leistung einer
Photovoltaikanlage einen eindeutigen Beweis dass die Finsternis auch hier stattfand ... ;-)
|
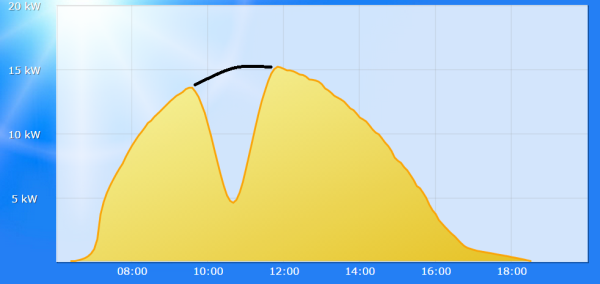
Die Aufzeichnung einer Anlage in Süddeutschland erlaubt es, die Resthelligkeit von 31
Prozent zu messen, in sehr guter Übereinstimmung mit den für diesen Standort
vorhergesagten 30 Prozent.
|
Sonnenfinsternis 2006 TBD
Die totale Sonnenfinsternis am 29.März 2006 dauerte von 07:30 bis 12:45 Uhr UT.
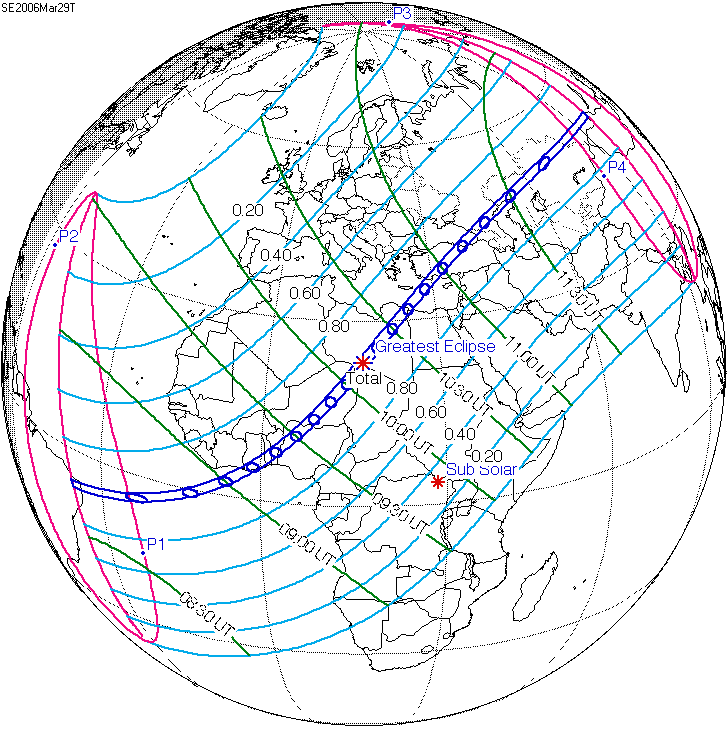
Zu Beginn fällt der Kernbereich des Schattens zunächst auf Brasilien, dann überquert er den Atlantik und
durchstreift Afrika von Ghana bis Libyen. Hier ist der Schattenwurf am stärksten ausgeprägt, der Kernschatten
hat einen Durchmesser von 183 Kilometern und die Finsternis dauert für einen Beoachter am Erdboden gute
4 Minuten. Der Schatten bewegt sich weiter über das Mittelmeer, die Türkei, Kasachstan, Teile Russlands,
bis an die Mongolei.
Von Deutschland aus war nur eine partielle Sonnenfinsternis zu beobachten, da der Kernschatten Deutschland
nicht berührte.
Die Animation durch einen Film aus Bildern des geostationären Wettersatelliten METEOSAT Second
Generation (MSG) zeigt die Wanderung des Mondschattens über die Erdoberfläche:
Informationen zum Film
Im Vis-Film (sichtbares Licht) ist der eigentliche Kernschatten kaum zu erkennen, dafür aber der große
Bereich des Halbschattens, der mehrere tausend Kilometer durchmisst. Um den Kernschatten darzustellen
reicht weder die Bildauflösung (768x576 Pixel für einen Erddurchmesser = 12.000 km) noch die Farbtiefe
von 256 Graustufen (je 8 Bit Farben im Rot-, Grün- und Blau-Kanal des Bildes) Das bloße Aufzeichnen eines
einzelnen Bildes nimmt ca. 12 Minuten in Anspruch, das jedes Bild vom Satelliten Zeile für Zeile ausgegelesen
wird.
Der Kernschatten wandert zu schnell, als dass er mit dieser Methode scharf aufgezeichnet werden könnte.
Im Infrarotfilm kann man vor allem in Nordafrika eine deutliche Temperaturverringerung während des Durchzuges
des Mondschattens sehen.
|

|
|
|
Aufnahme durch die Satellitenstation in Rönne
|

