Die Erdatmosphäre

Obgleich unsere Atmosphäre fûr Radiowellen transparent ist, ist ihr Einfluß nicht vernachlässigbar klein: Sie macht sich durch zusätzliches Rauschen - durch Wärmestrahlung - und bei höheren Frequenzen durch eine Abschwächung des Signals - durch Absorption der Luftmoleküle - bemerkbar. Da eine Sichtlinie bei niedriger Elevation durch eine größere Luftsäule geht als in Richtung Zenit, nehmen diese Wirkungen mit fallender Elevation zu. Misst man das Signal des 'leeren' Himmels auf 1.3 GHz bei verschiedenen Höhen über der Horizont, so erhält man eine Reihe von Stufen:

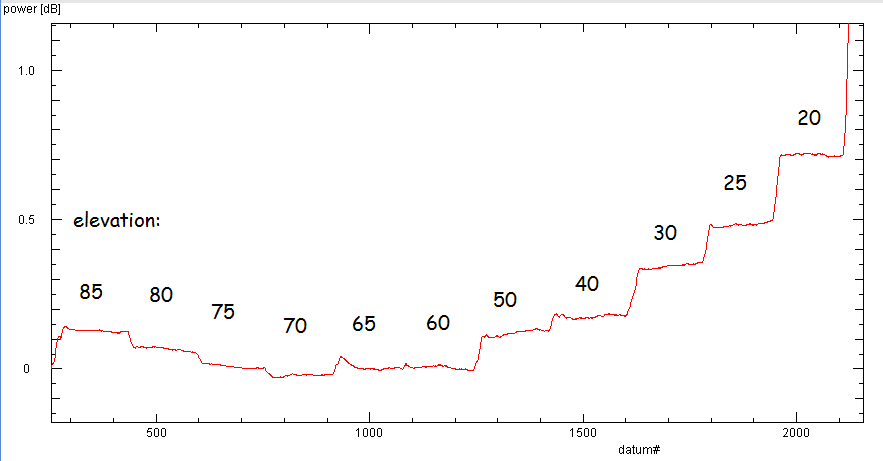
Dass das Rauschen bei Elevationen über ca. 70º wieder ansteigt, ist durch das Spill-over der Antenne bedingt (siehe dort). Sehen wir von diesem Effekt ab, so läßt sich die Zunahme des Rauschens zu niedrigen Elevationen quantitativ erklären und in folgender Weise auswerten. Da die dichten Schichten der Atmosphäre - die Troposphäre - sich bis nur etwa 8 km über dem Erdboden erstrecken, kann man ihre Dicke gegenüber dem Erdradius vernachlässigen, und sie als eine planparallele Schicht darstellen. Schaut man in Richtung Zenit, und habe die Luftsäule die Länge L, so ist die bei Elevation ε durchlaufene Luftsäule größer, nämlich L/sin ε . Trägt man nun die bei verschiedenen Elevationen gemessenen Werte gegen 1/sin ε auf, so ergibt sich eine Gerade:

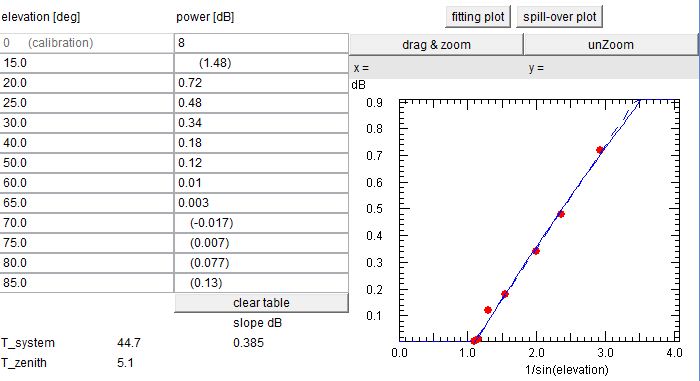
Hierbei sind die eingeklammerten Werte nicht berücksichtigt worden, wegen Spill-over und weil bei 15º die Antenne bereits Rauschen des Erdbodens aufnimmt.

Interpretation der Daten

Sie ergibt sich aus der Skizze des Prinzips:

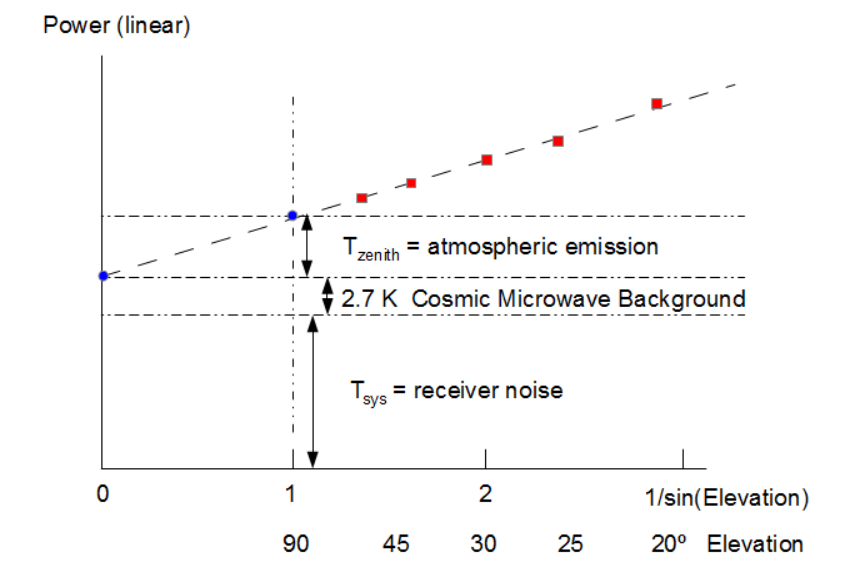
Die roten Quadrate deuten Messwerte an, die blauen Kreise weisen auf daraus extrapolierte Punkte. Das gemessene Signal setzt sich aus mehreren Anteilen zusammen:

Paßt man an die Datenpunkte eine Gerade an, so erhält man neben der Steigung m den Y-Achsenabschnitt b, den Wert bei 1/sin ε=0. Diesem Wert entspricht kein realer Winkel, aber den extrapolierten Messwert würde man erhalten, wenn keine Atmosphäre vorhanden wäre!

Die Messwerte sind ein Maß für die Leistung, aber gegeben in irgendwelchen, vom Messgerät bestimmten Einheiten. Wenn diese in dB (deziBel) vorliegen, müssen die natürlich erst in lineare Leistung umgewandelt werden (p = 10dB/10). Um sie in Antennentemperaturen auszudrücken ist der Skalenfaktor a zu bestimmen:

p(Quelle) = a (Tquelle + Tsky(ε) + Tsys + TCMB)
wobei hier alle Anteile einer Quelle, des Himmelshintergrunds, des Empfängerrauschens und des Mikrowellenhintergrunds aufgeführt seien. Dazu wird zunächst eine Flusskalibration durchgeführt: Die Antenne wird auf den Erdboden, ein Gebäude, oder - wie bei der 1 GHz Antenne - ein dichtes Gehölz gerichtet, das die gesamte Antennekeule mit seiner Wärmestrahlung ausfüllt (mit Tcal = 290 K):
p(cal) = a (Tcal + Tsys)
Hierbei fallen keine Anteile vom Himmel oder Mikrowellenhintergrund an. Aus der Prinzipskizze erkennt man:
b = a (Tsys + TCMB)
Daher ergibt sich der Skalenfaktor als
a = (p(cal) - b) /(Tcal - TCMB)
und damit erhält man die Systemtemperatur:
Tsys = b(Tcal - TCMB)/(p(cal) - b) - TCMB
Schließlich kann man wegen p(zenit) = m + b = aTzenit + b aus der Geradensteigung die Antennentemperatur im Zenit berechnen
Tzenit = m/a = m(Tcal - TCMB)/(p(cal) - b)

Ergebnisse

Für 1.4 GHz ergibt sich eine Zenittemperatur von ca. 5 K, die vom Wetter ziemlich unabängig zu sein scheint.

Messungen auf 24 GHz geben Zenittemperaturen von etwa 20..30 K. Allerdings fällt auf, daß die Meßwerte nicht auf einer Geraden liegen, sondern auf einer gekrümmten Kurve. Dies läßt sich als Wirkung der atmosphärischen Absorption, durch den Wasserdampf in der Luft, deuten. Dies wird näher untersucht (Okt. 2014) ...

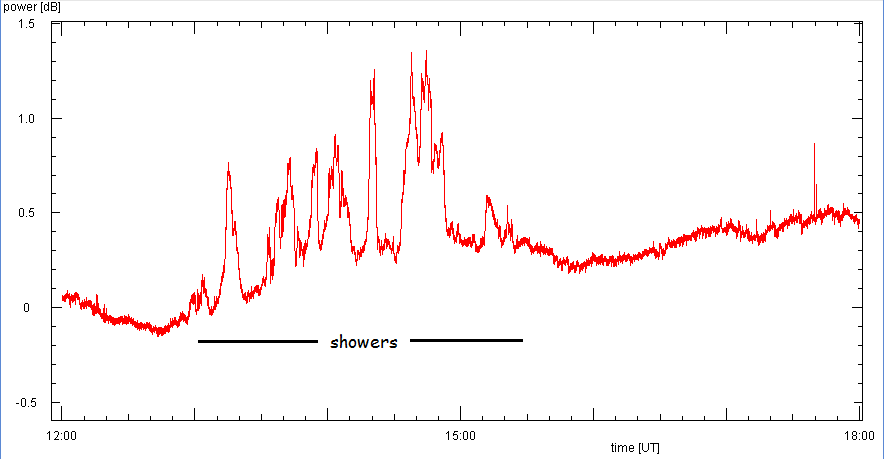
Wetter

Schließlich gibt es noch das Wetter: vorbeiziehende Regenwolken und Regenschauer können erhöhtes Rauschen durch die Wärmestrahlung des Wasserdampfs oder der Regentropfen verursachen. Hier ein Beispiel auf 24 GHz von ergiebigen herbstlichen Nachmittagsschauern: