The Milky Way

The Sun with its planets is but a small, ordinary star among the 10000 million other stars that make up our Galaxy. What we see of the Milky Way as a brightish band across the sky - if we look at it from a very dark place - is the light of all these stars. Almost all of the stars are located in a disk which rotates around the Galactic Centre (in the constellation of Sagittarius). At radio wavelengths the Galaxy looks somewhat different:

The band along the galactic equator is narrower and the radiation does not originate from stars, but from the gas which fills the space between the stars, and out of which stars are formed. This interstellar gas comprises several components of different temperatures. There is thin and very hot gas of several million Kelvin, which had been produced by exploding stars; there is warm and cool gas in ionized and neutral form, and clouds of cool (10 K) and dense gas, which contains a great diversity of molecules and out of which new stars can be born.

Ionized gas produces radio radiation as a thermal continuum and also a non-thermal continuum when electrons are deflected by the interstellar magnetic field into circular and helical orbits.

Neutral and molecular gas shows line emission from the characteristic spectral lines of the atoms and molecules. A special role is occupied by hydrogen because of its high abundance of 90 percent of the atoms of normal matter. The proton and the electron which moves around it both have an internal angular momentum, the 'spin'. When an hydrogen atom finds itself in a state where both spins are oriented in parallel, after a collision with another particle, the electron re-orients itself to the energetically more favourable anti-parallel orientation by radiating the excess energy in form of a radio wave at a sharply defined frequency of 1420.405751 MHz - which corresponds to a wavelength of about 21 cm.

The Solar System is located in about R_o = 8.5 kpc distance from the Centre, and moves approximately on a circular orbit with a velocity of about v_sun = 210 km/s. In the 21 cm line of hydrogen one can observe clouds of neutral gas everywhere in the Milky Way, and from the Doppler shift of the line one can measure the radial velocity. Thus it is not only possible to map the interstellar neutral gas of the Galactic Disk, but also to measure the rotation of the disk.

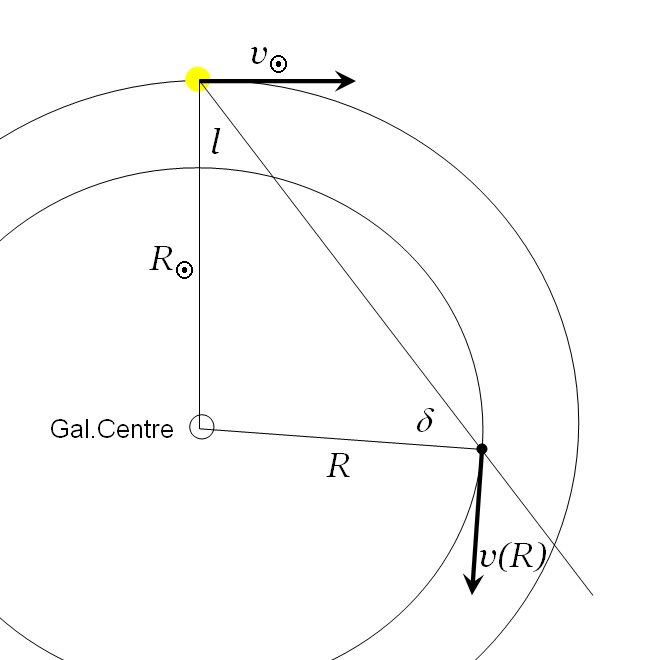
Consider a gas cloud which lies in direction of galactic longitude l with a distance R from the centre and moves on a circular orbit with velocity v(R). It will appear to us at a radial velocity (using the sine law of planar triangles): v_rad = (v(R) * R_sun/R - v_sun) * sin l Therefore every position on this line of sight is characterized by its radial velocity. When we observe emission at a certain velocity, we may draw conclusions where the cloud will be.

In a JavaScript tool we can display graphically the above formula, and thus show in the Galactic Plane those regions, in which gas clouds are seen from the Sun (yellow circle, r_sun = 8.5 kpc) with positive or negative radial velocity:

Rotation curve
V_rot(r) = V_sun + dvdr*(r-r_sun)
V_sun [km/s]
dvdr [km/s/kpc]

line of sight:
Galactic longitude

Mouse position:

Looking towards l=50°, which takes the line of sight through the region inside the solar orbit, the emission is seen redshifted, i.e. at frequencies below the theoretical line frequency. From larger distances one picks up blue-shifted emission.
The plot along the line of sight shows how the radial velocity depends on the distance: at first it increases, reaches a maximum, and then decreases monotonically and becomes negative.
An observer on our southern hemisphere would see the similar behaviour towards l=310, but with the opposite sign!
Looking towards l>90°, i.e. only outside of the solar orbit, there is neither a change of sign nor a maximum. The radial velocity decreases (or increases) monotonically with distance.
Gas clouds in direction of the Galactic Centre, the anti-centre (l=180°), and on the

Rotation Curve

Since for any lines of sight that pass through the interior of the solar orbit, viz. 0°<l<90° and 270°<l<360° the radial velocity has a maximum value, it is possible to measure the rotation of the Milky Way: Maximum radial velocity v_max have clouds which are located where the line of sight touches the circular orbit for which it is the tangent. At galactic longitude l one measures the rotational velocity for the radius R = R_sun sin l: v(R) = v_max + v_sun sin l

Spiral arms

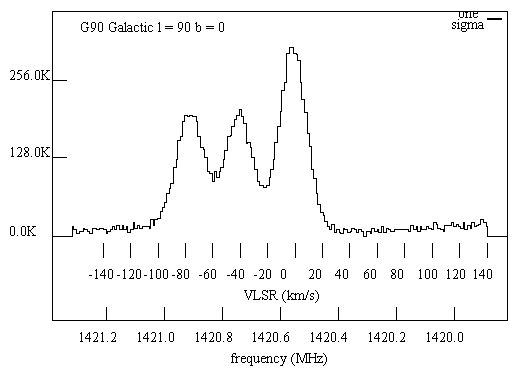
Observing in direction l=90° and b=0° one obtains this spectrum, which shows several emission features. Since the 21 cm line is intrinsically a very narrow line, the spectral features are produced by the different radial velocities (from -100 to +20 km/s) of the gas clouds.

The individual "bumps" are interpreted as assemblies of gas clouds which move together and form spiral arms
The width of the bumps of about 20 km/s shows that the clouds inside such an arm have some individual motion. They move with respect to the average speed of the arm with this velocity in random directions.

Our Galactic Survey 2013/15

Using the 9 m dish, we conducted a sky survey in the light of the 21 cm line. The observations were done by drift scans: The telescope was pointed to a fixed position and for the next couple of hours spectra were continously recorded of those regions which pass by. From the known pointing position and the time the galactic coordinates of every spectrum is computed. The reduced spectra are added to the corresponding bins in longitude and latitude, so that one obtains an average of 100..600 spectra for each position.

To the visualization tool

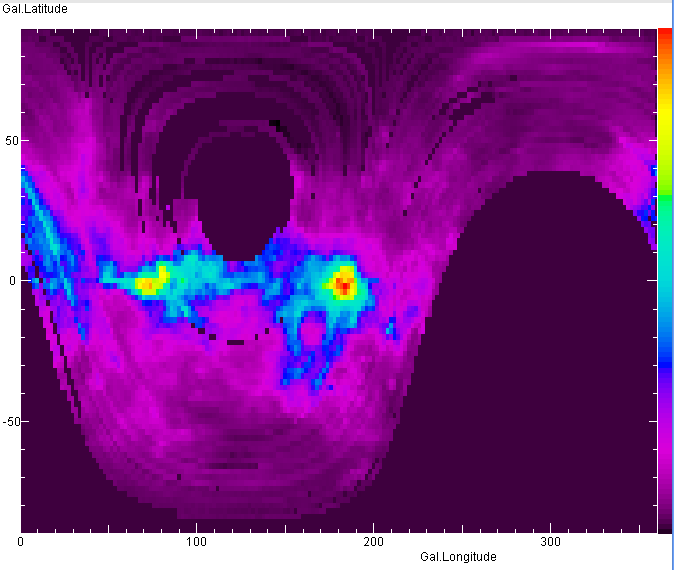
	The sky distribution of gas with zero radial velocity, from the AllSky dataset.
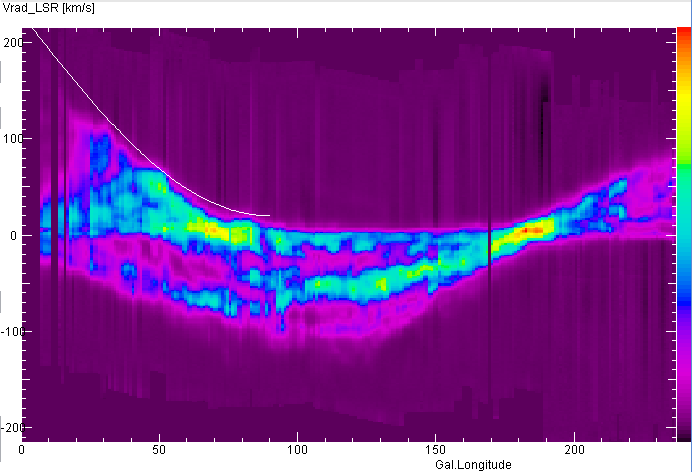
	A view of the Galactic Plane: The intensities are represented in a false colour map as a function of longitude and radial velocity. The white curves show the expected dependence of radial velocities on longitude for a constant value of the rotational speed of 230 km/s. The good match of this curve with the border for the emission seen between l=0 and 90° demonstrates that the rotational velocity is independent of the distance from the Galactic Centre, which is taken as one of the indicators of the presence of 'Dark Matter'
	Enlarged view of the inner Galactic Plane showing features from spiral arms which lie inside the solar orbit. Three of them are emphasized by white dots. Note that at several longitudes the intensity changes abruptly, because the sensivity of the instrument may vary slightly between different days.
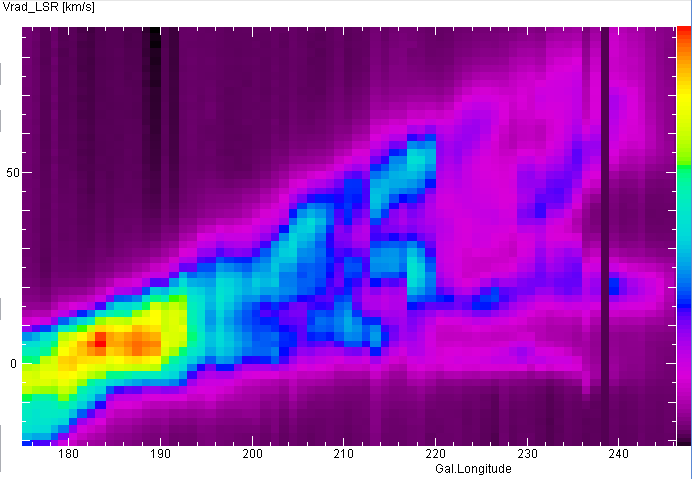
	Enlarged view of the Galactic Plane in the direction opposite from the Galactic centre. At longitude 180° all emission features cluster at 0 km/s, because towards this direction we see gas which moves parallel to our own motion, so that the radial velocity is near zero, except for small deviations from a circular motion. For longitudes 200 .. 240° a number of spiral arms can be seen, all of them lying outside the sun's orbit. The intensity decreases towards 240°, as the antenna needs to be pointed close to the horizon. Beyond 240° no observations from our Northern latitude are possible.
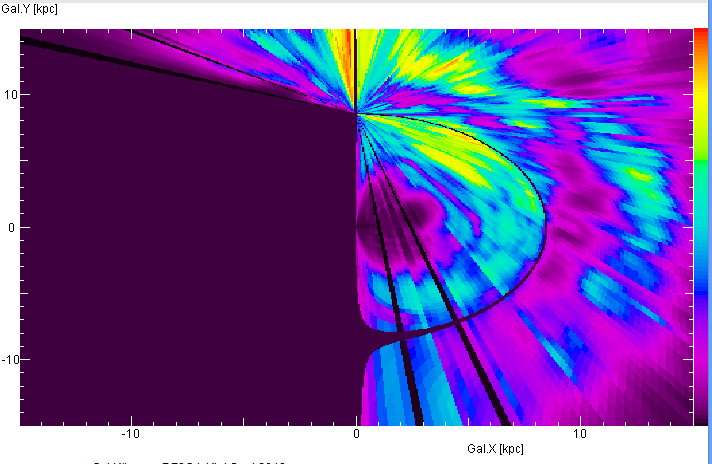
	If one assumes a model for the rotation of the Galaxy, one can compute from the radial velocity of a gas cloud its distance from us. In this way one may construct a map of the interstellar gas, as one would see it, if one could look onto the galactic disk from the outside. Most prominent is the spiral arm which lies outside of the orbit of the sun (marked by the black circle).
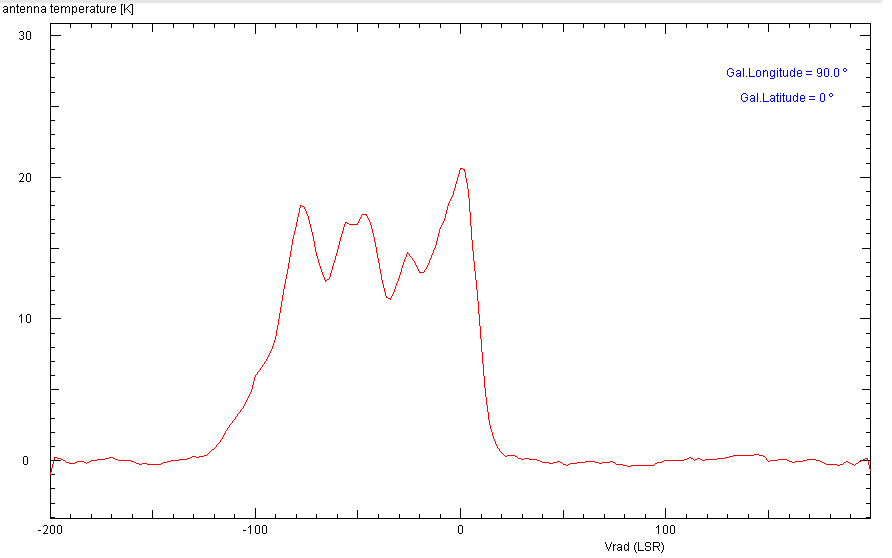
	The spectrum in the plane at l=90° shows the emission from local gas (the feature at 0 km/s) and 4 to 5 blue-shifted features from the gas of the spiral arms outside the solar orbit.
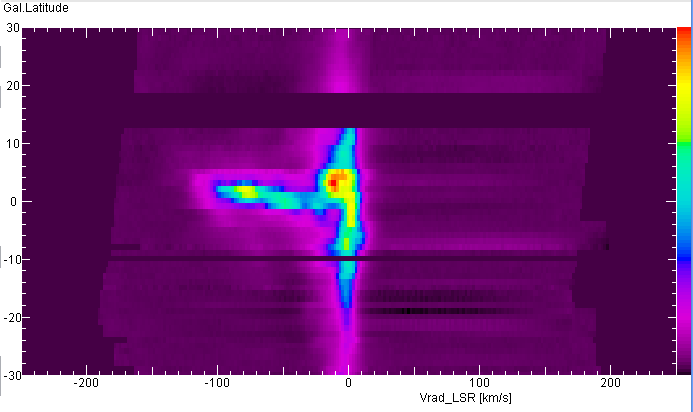
	The latitude-velocity map at l=90° shows emission near 0 km/s and at all latitudes. This is the interstellar hydrogen in our near vicinity all around us. At negative radial velocities and near the plane one notes a number of bright knots - like the features in the spectrum above, extending up to -100 km/s: This is the gas of the spiral arms outside the solar orbit. The fastest knot lies a slightly higher latitude, about 2°, than the slower ones. This means that the Galactic Disk is not in a single plane, but it is warped: Its outer parts lie at l=90° above the Plane.