Pulsars
Pulsars are rapidly rotating neutron stars, whose magnetic axis is inclined with respect to
its rotation axis. A neutron star is the very compact (10 km radius) left-over of the core
of a massive star (10 to 100 solar masses), when this star explodes as a supernova at the
end of its life. At the time of the explosion all the fuel for the nuclear fusion processes
has been exhausted, and the core of the star consists of iron, the most stable element.
Since energy production by fusion dies out, so does the high pressure which so far had
counteracted the weight of the stars outer layers. As a consequence, the star collapses
rapidly onto its centre, but the colliding gas layers bounce back, some nuclear fusion
processes can ignite, and the star becomes a bright as an entire galaxy: a supernova.
What is left-over from such a catastrophic event, is a black hole or a neutron star, formed
from the matter of the star's central region. In a neutron star, the iron nuclei are
squeezed together to form what is essentially a plasma of neutrons.
Like a figure scater doing a pirouette spins faster when (s)he brings the arms close to the body,
due to the conservation of angular momentum, the collapse of the slowly rotating progenitor
star results in the neutron star to spin with periods of 1 second and faster.
During the final collapse, the magnetic fields of the star are also squeezed into a small
volume, thus the field strength at the surface of the neutron star is extremely high:
about 1010 Tesla, while our Sun has a field of about 10-4 Tesla!
Because of the rapid rotation the rapidly changing strong magnetic fields induce a huge
electric field of about 1011 V/m, which easily overcomes the gravitational pull
on charged particles, and electrons and positrons are pulled away from the neutron star's
surface. As charged particles can only move in a spiral path around and along the curved
magnetic field lines, they are pulled into higher regions of lower density. Their curved
path also causes them to radiate electromagnetic waves which comes out in a narrow cone
parallel to the magnetic field lines. Thus the radiation is concentrated in a direction
of the magnetic axis.
If the magnetic axis is inclined with respect to the rotation axis, the neutron star sends
out beams of radiation, from its magnetic north and south poles. Due to the rotation,
the beams point to two large circles in space, just like the light beam of a lighthouse.
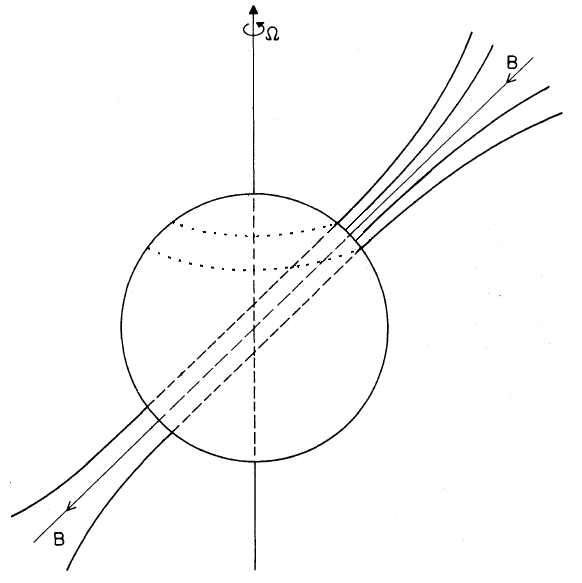
Schematic sketch of a neutron star rotating about the Ω-axis, but with an inclined
magnetic axis, indicated by the field lines B near the magnetic poles. Electrons and positrons
move along the field lines and produce beams of radiation in both directions of the magnetic
axis. The star's rotation
takes these beams around (adapted after Ruderman and Sutherland, 1975).
As the charged particles move into regions high above the neutron star's surface where the density
is lower, their radiation is centered at lower frequencies. In this way they produce radiation
over a wide range of frequencies (from the X-rays to radio waves), as they travel through
the neutron star's magnetosphere.
|
|
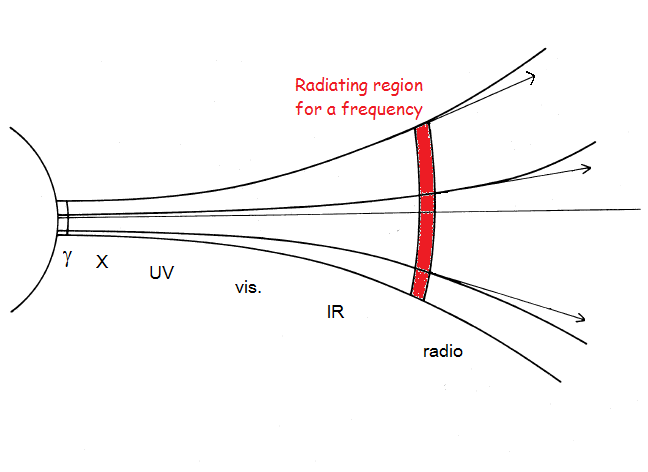
The frequency of the radiation which is produced in a zone depends on the height
above the neutron star's surface: γ and X rays are produced close to the
surface, radio waves at greater heights, where the density is lower
(adapted after Ruderman and Sutherland, 1975).
|
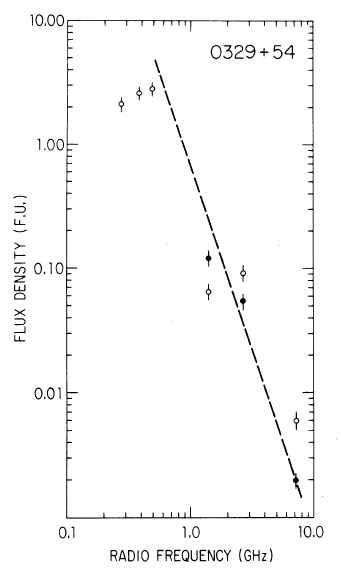
The radio flux density of the pulsar B0329+54 decreases with frequency
(from Backer and Fisher, 1974; 1 f.u. (flux unit) = 1 Jy).
|
If our Earth happens to be in a direction towards which this beam may point, we observe a
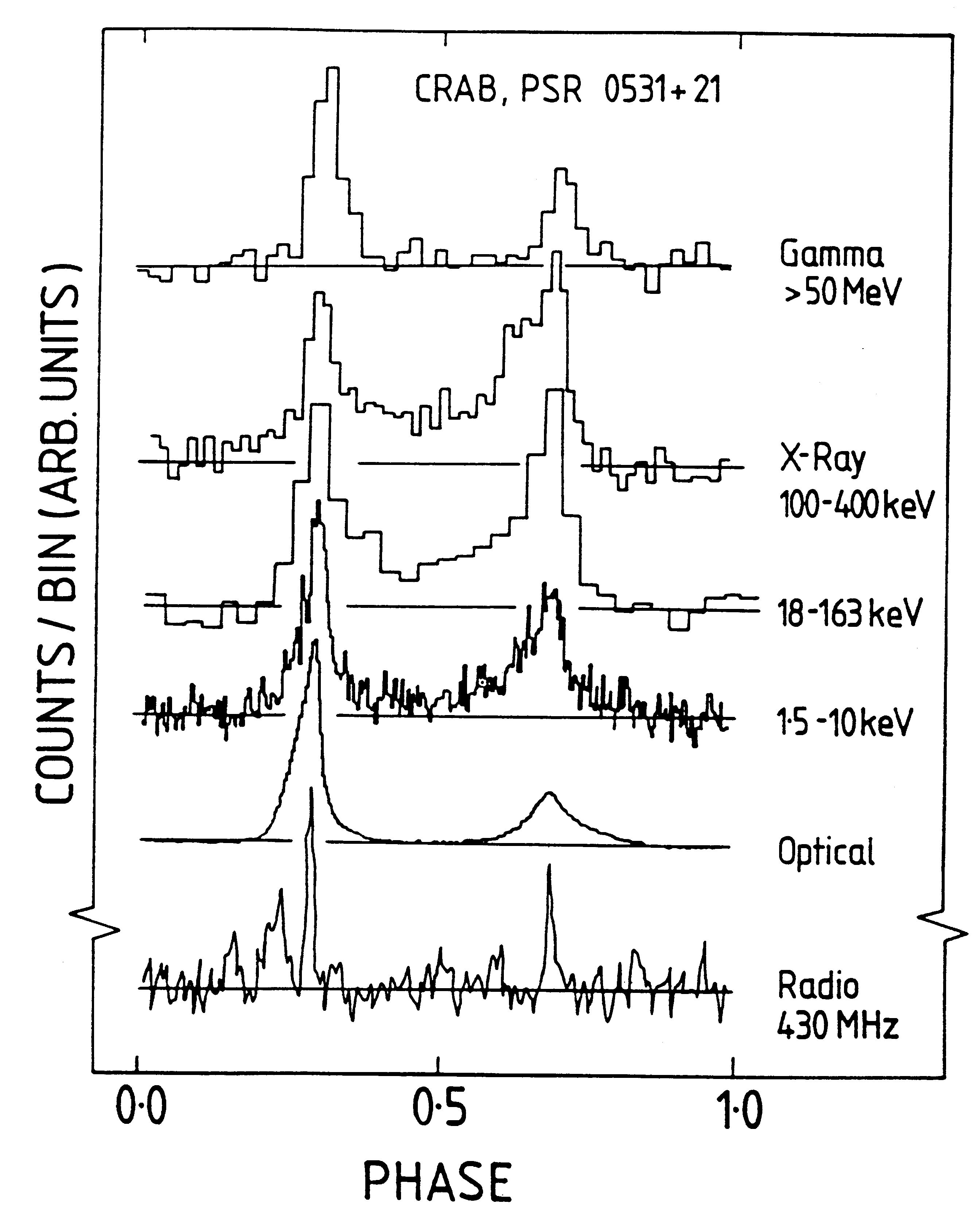
periodic flash of radiation: a pulsar. A famous pulsar is in the centre of the Crab nebula:
|
|
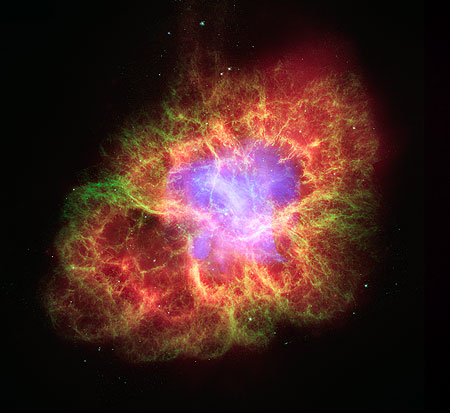
The Crab nebula, the gaseous left-over of a supernova explosion. This is
both gas ejected by the dying star and gas filaments formed by the collision
with the ambient interstellar gas. The composite image shows the emission in the X-rays
from synchrotron radiation (blue) and by emission lines in the optical
(green) and infrared (red).
|
In the centre of the nebula there is the Crab pulsar, which emits
radiation pulses in the whole range from γ-rays and X-rays to radio
waves, with a period of 0.0333 s
|
See here for more Technical Details about Pulsar Observations at DL0SHF
Jodrell Bank Observatory has a very nice collection of the
Sounds of Pulsars.
Observations: B0329+54
This is the strongest pulsar in the northern skies with a (true) period of 0.714 518 663 98 s
and a flux density of 200 mJy at 1.4 GHz.
|
|
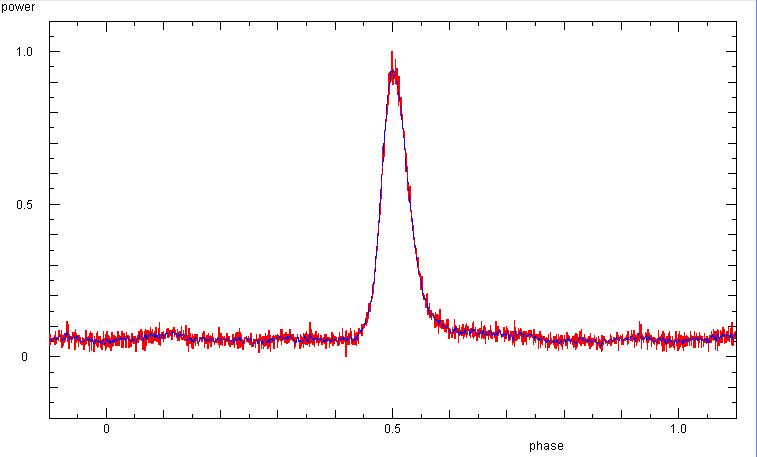
Phase diagram (or folded light curve) from the last 8 min part from an
observation on 2 nov 2014 with
a sampling rate of 1 kHz. The 'old' instrument configuration with the HP437B
power meter has a response time of 50 ms, which broadens the pulse.
|
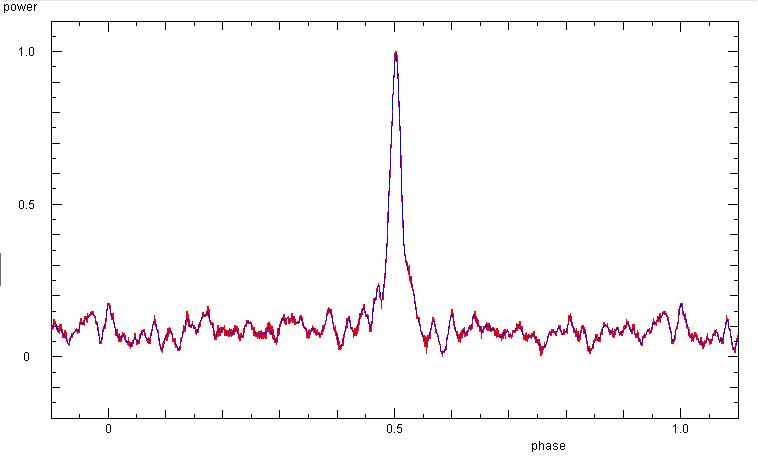
Phase diagram from 6.5 min of data, averaged over 10 samples taken at 30 kHz rate.
This was done on 30 sep 2015, with the 'new' instrument configuration of a
EP441 power meter. With the better time resolution the main pulse is sharper,
and the subpulses before and behind the main pulse are discernible.
|
|
|
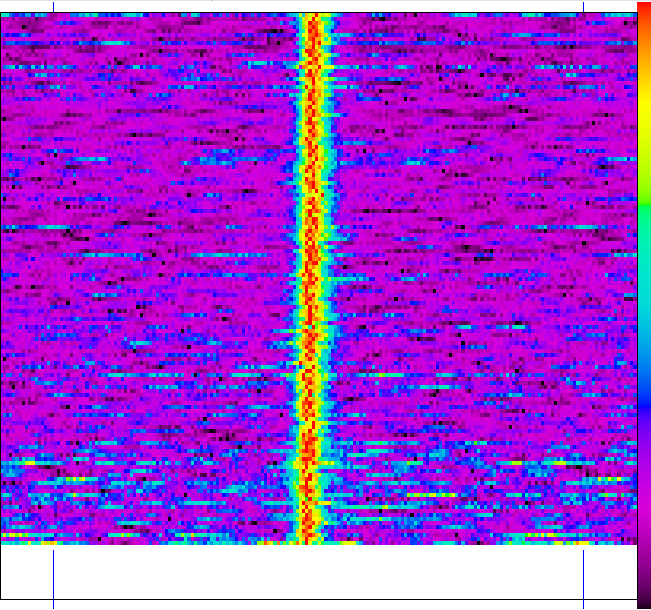
Waterfall plot of the data of 2 nov 2014.
|
Waterfall plot of the data of 30 sep 2015.
|
|
|
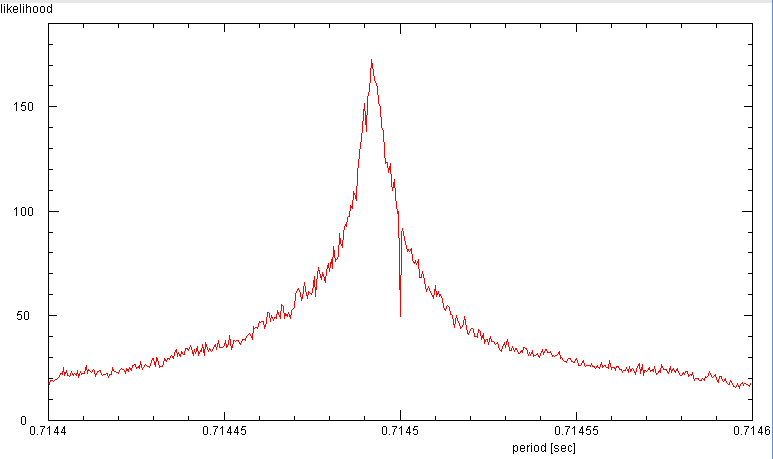
In a 2 hour section with high signal to noise from 26 oct 2015, the period
of B0239+54 is found to 0.714492 s. Data was taken with 40 kHz sampling rate
and the averages were recorded at 500 Hz.
|
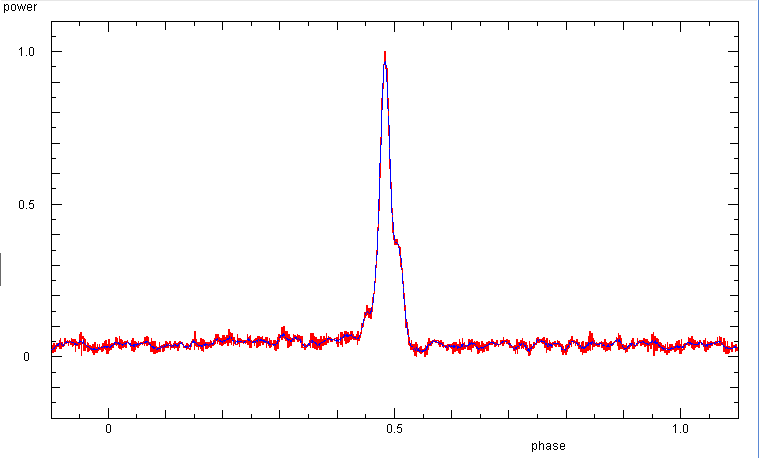
The phase diagram shows the weak sub-pulses before and after the main pulse.
|
Observations: B0950+08
The second brightest is B0950+08 with a (true) period of 0.253 065 068 19 s
and a flux density of 85 mJy at 1.4 GHz. The best result was obtained on 30 sep 2015
during a 40 min observation, averaging over 10 samples taking at a rate of 30 kHz.
This gives about 7.2 million data points.
|
|
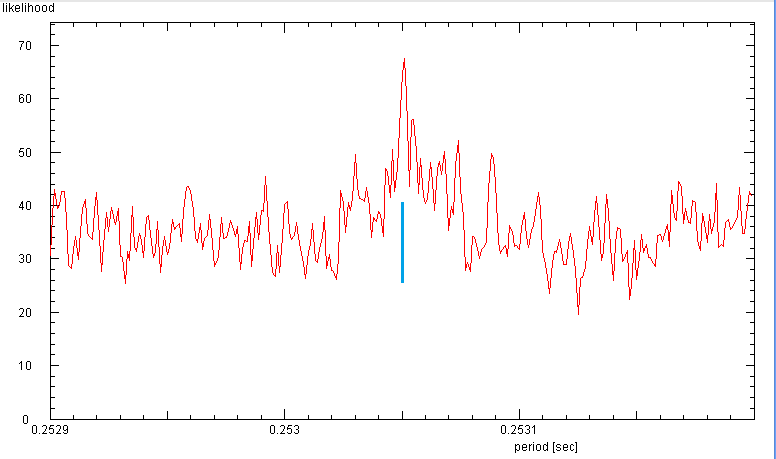
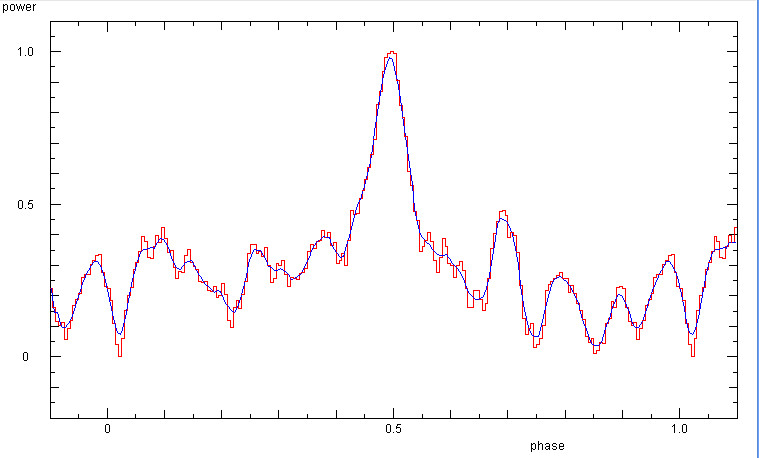
Searching for the period of B0950+08: The faint signal requires many data.
The search for the period needs to be confined in a narrow range, as only
the exact period will make a reasonable phase diagram. The best fit is found
with the period of 0.25305 s.
|
Phasediagram of B0950+08 for a period of 0.25305 s.
|
In the waterfall plot of this data set the pulsar signal appears only clearly, if one
choses a time intervall of 300 s from which phase diagrams are computed. When the pulses
are made to form a vertical line, i.e. if the pulses are made to appear at the same
phase, one gets the period of 0.253049 s
period

Observations: B1933+16
The third brightest is B1933+16 with a (true) period of 0.358 736 248 270 s
and a flux density of 40 mJy at 1.4 GHz. On 25 sep 2015 a 30 min observation
with averaging over 10 samples at 50 kHz rate yields this result:

|

|
Search for the period of B1933+16: Again, the search range needs to be rather
small around the expected value. The quite prominent peak at 0.358388 s does not
show a pulsar signal, but 0.35877 s is the pulsar
|
Phase diagram of B1933+16 with a period of 0.35877 s
|
In the waterfall plot of this data set the pulsar signal appears only clearly, if one
choses a time intervall of 300 s from which phase diagrams are computed. When the pulses
are made to form a vertical line, i.e. if the pulses are made to appear at the same
phase, one gets the period of 0.35877 s
period

Observations: Scintillations of B0329+54
On their way from the pulsar to the Earth, the radio waves pass through the interstellar
medium, which contains clouds of warm and hot plasma, which strongly influences the radio
waves. Refraction causes them to change their direction. The radio flux that arrives at Earth
is the result of the superposition of waves that are affected in varying degrees. Thus the
measured flux depends on the situation in he interstellar medium along the line of sight
to the pulsar. The movement of the pulsar and of the plasma clouds causes the radio flux
to flicker, in the same way as the turbulent motion of air packets in our atmosphere
causes stellar light to flicker.
This causes the signal from the normally bright pulsar B0329+54 to become much fainter
for times, which makes testing and optimising the receiving system quite challenging.
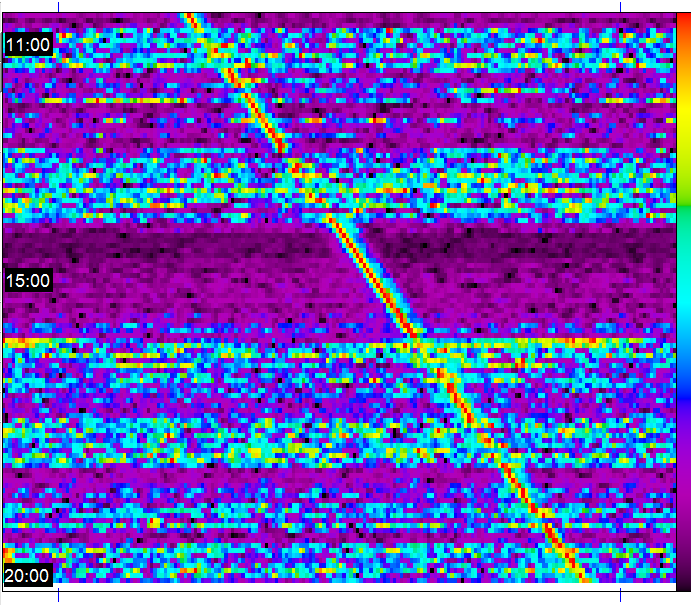
Here is a waterfall showing what happened during 10 hours on 26 oct 2015:
for one hour around UT 15:00 the pulsar B0329+54 was exceptionally strong.
At other times it changed between a reasonably good signal and being buried in the
noise. Although this diagram is done with too short a period, which causes the line
of the pulses to drift to the right, one can easily follow the coming and going
of the signal:
B0329+54 can be used to study scintillation, by continously measuring its signal, and
observing the time variation of the strength of the pulse with respect to the noise.
This is done for several days in autumn 2015, during which all instrumental details
are kept unchanged. The data is sampled at 40 kHz, but averaged over 80 data points,
so that the data are recorded with a rate of 500 Hz, which makes smaller file lengths.
From 1 minute sections of the raw data, phase diagrams are computed and the ratio of the
height of the highest peak to the standard deviation of the background around this maximum
is taken as the signal to noise ratio.
From the entire data set the strong variation of the signal to noise ratio is apparent.
It can vary between about 20 to close to 1.
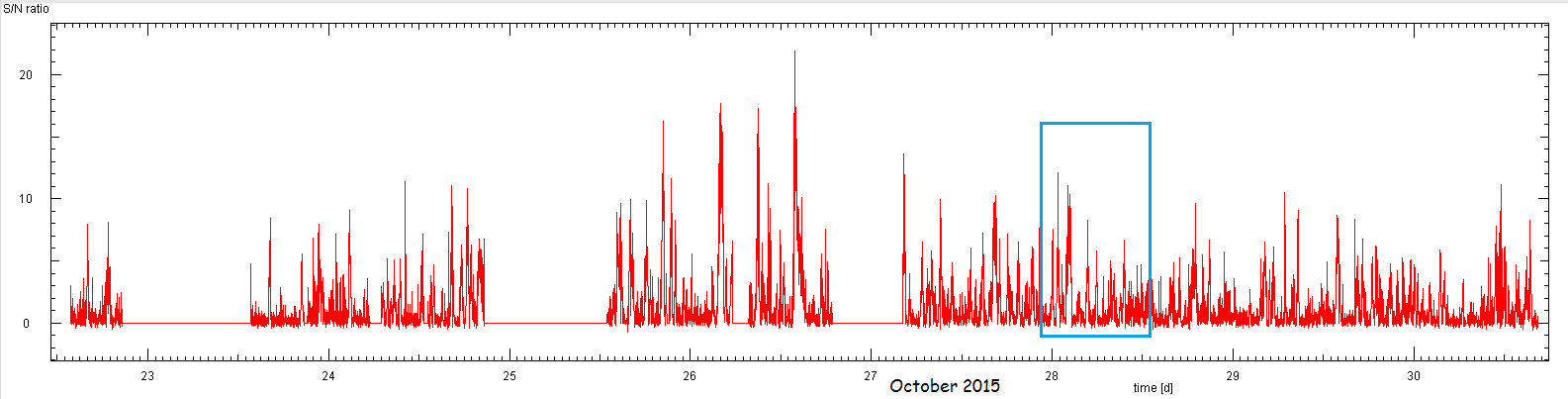
During a time span of 12 hours, the pulse may be present for a few minutes or as long as
an hour, only to suddenly disappear in the noise.


|
|
The autocorrelation function of the entire data set. The width of the
peak at zero time offset shows that the average duration of an interval of
high signal to noise ratio is less than 30 min. Also, the peaks at 5 and 7.5 hours
time offset indicat that there is a slight chance to have another stretch of
strong pulses after 5 or 7.5 hours. As these peaks a very low, it means that
there is no periodicity in the occurrence of good pulsar receptions.
|
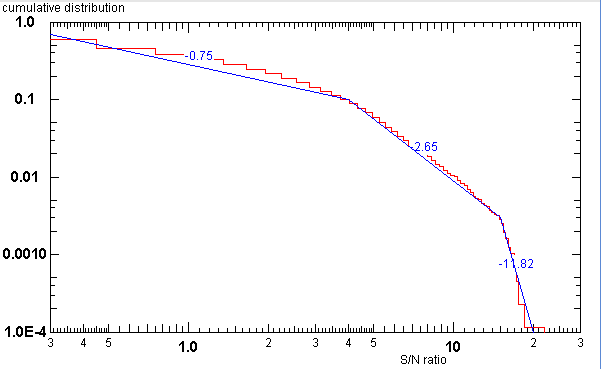
The cumulative distribution function of the signal to noise ratio in the
entire data set. It shows that conditions with high S/N ratio are very rare
occasions ... this diagram may permit some interpretation of the signal
level fluctuations and their nature (work to be done!)
|